Nelineárna dátová štruktúra pozostáva zo zbierky prvkov, ktoré sú rozložené v rovine, čo znamená, že medzi prvkami nie je taká sekvencia, ako existuje v lineárnej dátovej štruktúre.
Porovnávacia tabuľka
| Základ pre porovnanie | strom | graf |
|---|---|---|
| cesta | Len jeden medzi dvoma vrcholmi. | Je povolená viac ako jedna cesta. |
| Koreňový uzol | Má presne jeden koreňový uzol. | Graf nemá koreňový uzol. |
| Loops | Žiadne slučky nie sú povolené. | Graf môže mať slučky. |
| zložitosť | Menej zložité | Komplexnejšie |
| Traverzné techniky | Predobjednávka, In-order a Post-Order. | Vyhľadávanie v hĺbke a hĺbkové vyhľadávanie. |
| Počet okrajov | n-1 (kde n je počet uzlov) | Nie je definované |
| Typ modelu | hierarchický | sieť |
Definícia stromu
Strom je konečná zbierka dátových položiek, zvyčajne označovaných ako uzly. Ako už bolo spomenuté vyššie, strom je nelineárna dátová štruktúra, ktorá usporadúva dáta v triedenom poradí. Používa sa na zobrazenie hierarchickej štruktúry medzi rôznymi dátovými prvkami a organizuje údaje do pobočiek, ktoré súvisia s informáciami. Pridanie novej hrany do stromu vedie k vytvoreniu slučky alebo obvodu.
Existuje niekoľko typov stromov, ako je binárny strom, binárny strom vyhľadávania, strom AVL, závitový binárny strom, B-strom atď. Kompresia dát, ukladanie súborov, manipulácia s aritmetickým výrazom a herné stromy sú niektoré aplikácie stromu dátová štruktúra.
Vlastnosti stromu:
- V hornej časti stromu je označený uzol známy ako koreň stromu.
- Zostávajúce položky údajov sú rozdelené na disjunktné podsúbory označené ako podstrom.
- Strom sa rozširuje smerom dole.
- Strom musí byť pripojený, čo znamená, že musí existovať cesta z jedného koreňa na všetky ostatné uzly.
- Neobsahuje žiadne slučky.
- Strom má hrany n-1.
Existujú rôzne pojmy spojené so stromami, ako je koncový uzol, okraj, úroveň, stupeň, hĺbka, lesy atď. Medzi týmito výrazmi sú niektoré z nich opísané nižšie.
- Okraj - linka, ktorá spája dva uzly.
- Stupeň - strom je rozdelený na úrovne tak, že koreňový uzol je na úrovni 0. Potom sú jeho bezprostredné deti na úrovni 1 a jeho bezprostredné deti sú na úrovni 2 a tak ďalej až do terminálu alebo uzla listov.
- Titulok - Je to počet podstrán uzla v danom strome.
- Hĺbka - je to maximálna úroveň akéhokoľvek uzla v danom strome a tiež známa ako výška .
- Uzol terminálu - uzol najvyššej úrovne je uzol terminálu, zatiaľ čo ostatné uzly okrem terminálu a koreňového uzla sú známe ako neterminálne uzly.
Definícia grafu
Graf je tiež matematickou nelineárnou dátovou štruktúrou, ktorá môže predstavovať rôzne druhy fyzickej štruktúry. Pozostáva zo skupiny vrcholov (alebo uzlov) a množiny okrajov, ktoré spájajú oba vrcholy. Hrany na grafe sú reprezentované ako bod alebo kruhy a hrany sú zobrazené ako oblúky alebo segmenty riadkov. Hrana predstavuje E (v, w), kde v a w sú dvojice vrcholov. Odstránenie okraja z obvodu alebo pripojeného grafu vytvára subgraf, ktorý je strom.
Grafy sú rozdelené do rôznych kategórií, ako sú usmerňované, nesmerované, prepojené, nepripojené, jednoduché a viacgrafové. Počítačová sieť, dopravný systém, graf sociálnych sietí, elektrické obvody a plánovanie projektov sú niektoré aplikácie grafovej štruktúry dát. Používa sa tiež v riadiacej technike pomenovanej ako PERT (technika hodnotenia a hodnotenia programu) a metóda CPM (kritická cesta), v ktorej sa analyzuje štruktúra grafu.
Vlastnosti grafu:
- Vrchol v grafe môže byť spojený s ľubovoľným počtom iných vrcholov pomocou okrajov.
- Hrana môže byť smerované alebo nasmerované.
- Hrana môže byť vážené.
V grafe tiež používame rôzne pojmy, ako sú priľahlé vrcholy, cesta, cyklus, stupeň, pripojený graf, kompletný graf, vážený graf atď. Poďme porozumieť niektorým z týchto výrazov.
- Priľahlé vrcholy - vrchol a je vedľa vrcholu b, ak existuje hrana (a, b) alebo (b, a).
- Cesta - cesta z náhodného vrcholu w je susediacou sekvenciou vrcholov.
- Cyklus - Ide o cestu, kde sú prvé a posledné vrcholy rovnaké.
- Stupeň - Je to veľa okrajov, ktoré dopadajú na vrchol.
- Pripojený graf - Ak existuje cesta z náhodného vrcholu na akýkoľvek iný vrchol, potom tento graf je známy ako pripojený graf.
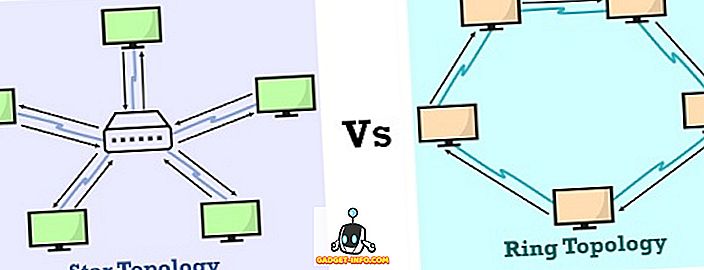
Kľúčové rozdiely medzi stromom a grafom
- Vo stromu existuje iba jedna cesta medzi dvoma vrcholmi, zatiaľ čo graf môže mať jednosmerné a obojsmerné cesty medzi uzlami.
- V strome existuje presne jeden koreňový uzol a každé dieťa môže mať len jedného rodiča. Oproti tomu v grafe neexistuje koncept koreňového uzla.
- Strom nemôže mať slučky a samočinné slučky, zatiaľ čo graf môže mať slučky a samočinné slučky.
- Grafy sú zložitejšie, pretože môžu mať slučky a samočinné slučky. Naproti tomu stromy sú v porovnaní s grafom jednoduché.
- Strom prechádza technikami vopred objednanými, v poradí a po objednávke. Na druhej strane, pre traverzovanie grafov používame BFS (Breadth First Search) a DFS (Depth First Search).
- Strom môže mať hrany n-1. Naopak, v grafe neexistuje preddefinovaný počet okrajov a záleží od grafu.
- Strom má hierarchickú štruktúru, zatiaľ čo graf má sieťový model.
záver
Graf a strom sú nelineárna dátová štruktúra, ktorá sa používa na riešenie rôznych zložitých problémov. Graf je skupina vrcholov a okrajov, kde okraj spája pár vrcholov, zatiaľ čo strom je považovaný za minimálne pripojený graf, ktorý musí byť pripojený a bez slučiek.
